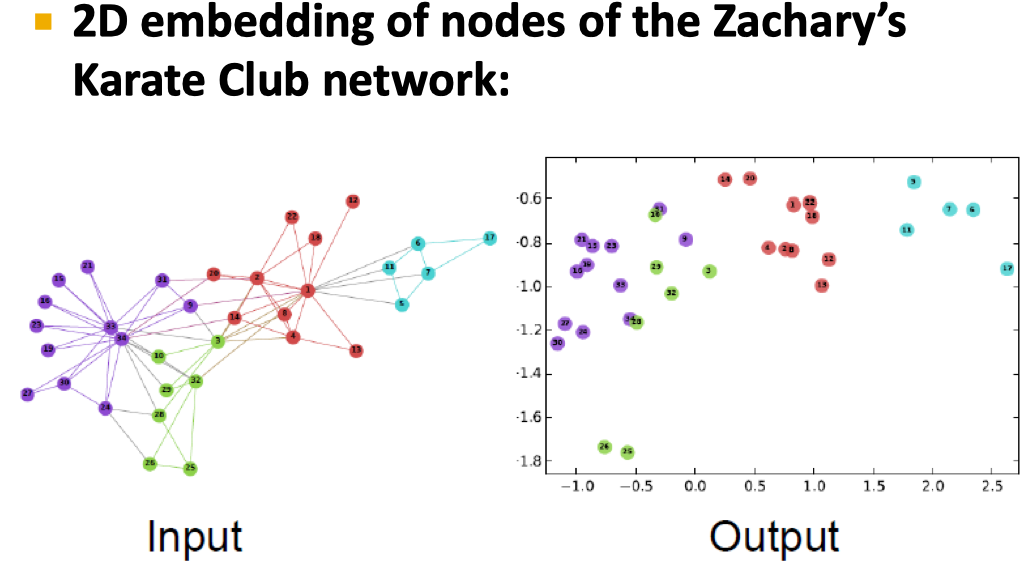
[CS224W]Embedding is All You Need: Node Embedding

零.前言

不得不说，优雅到令人心疼的思路。但是，除了博客中的这些经典工作，个人强烈建议了解下metapath2vec的工作，在近年来的很多学术和工业界的工作中，metapath2vec都是靓丽的存在。此外，这篇博客中，个人将知识表示和节点表示放在一块儿讨论，都属于representation learning的问题。

一.你需要啥样的Node Embedding？

在之前的博客中，已经反复提到Node Embedding的目的。这里用一张图的方式再一次重申，如下：

为了learn到一个不错的Node Embedding，需要定义Node Similarity，那么如何定义呢？

• 如果两个节点是linked的，应该有相似的Embedding吗？
• 如果两个节点share相同的neighbors，应该有相似的Embedding吗？
• 如果有相似的“structural roles”，应该有相似的Embedding吗？

假设利用无监督的方式得到节点Embedding，有以下几个优点：

（1）不利用节点label

（2）不利用节点feature

（3）直接利用节点的坐标序列得到能够保持网络结构的特征

（4）task independent

二.Random Walk（->DeepWalk）

无监督方式的核心是Random Walk。优点如下：

通过Random Walk，将图的问题转化为一个序列问题，继而可以采用Word2Vec的思想得到表征。既然是一个序列问题，那么这里的核心是序列怎么得到？对于DeepWalk而言，是采用一个固定长度，无偏的随机采样序列。

从直觉上来看，这一定不是最好的，是吗？

三.Biased Walks(->Node2Vec)

Node2Vec的核心思想是利用灵活的，有偏的随机采样序列。目的是在loca和global特征之间能够trade off。具体的做法是基于BFS和DFS。如下：

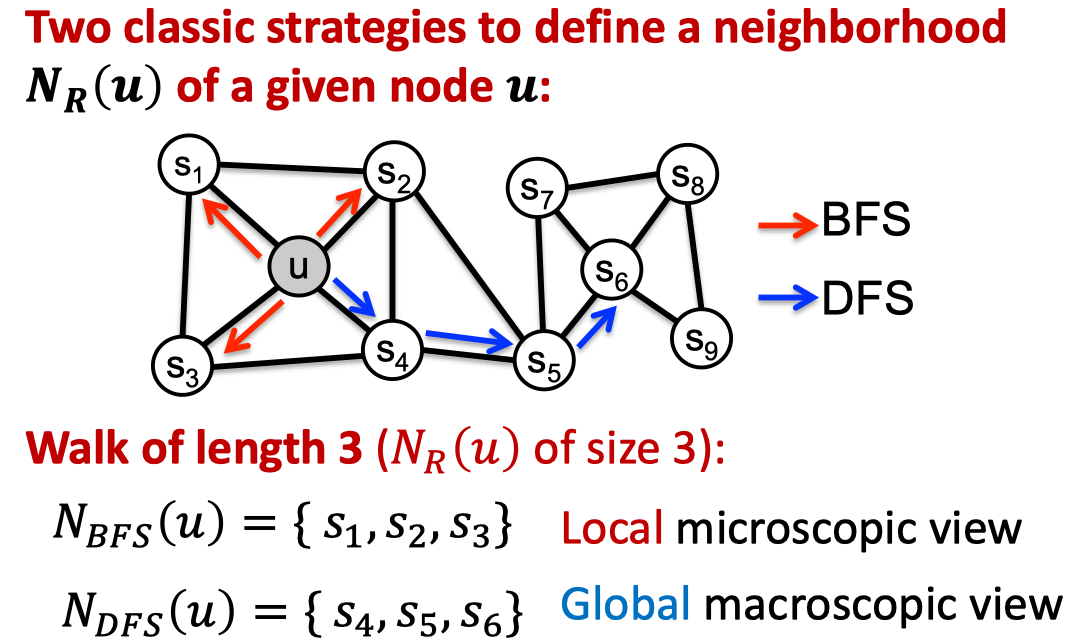
其中，BFS提供了关于neighbor的微观视角，DFS提供了关于neighbor的宏观视角。

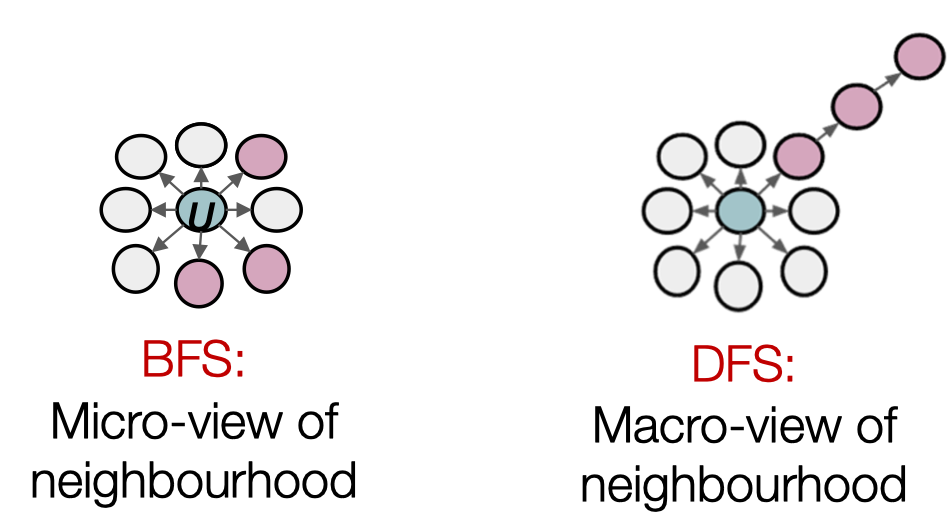
截止现在，如何回答node similarity这个问题呢？

（1）如果两个节点是connected的，那么是相似的

（2）如果两个节点的neighbor是overlap的，那么是相似的

（3）基于Random Walk的方法

但是，没有一种方法适用于所有。Node2Vec在节点分类任务上表现更好，但是其他的方法在链接预测任务上表现良好，相似性的运用取决于自己的应用场景。但是无论怎样，基于Random Walk的方法的高效性，是真滴香。

启发：解决一个问题，刚开始用一个比较直白，朴素的方式来理解并尝试解决，之后逐步用并不显然，但是也能从一个方面反映问题本质的方法来求解，前提是这样的方法能够带来肉眼可见的提升。最后，要回过头来看，这种方法到底解决了啥子问题？

四.不能只有节点的表征，还要图的表征？

（1）对节点特征求和完事儿

（2）引用”virtual node”，代表subgraph，然后用得到节点表征的方式来做，本质上是考虑graph内生的层次性

（3）Anonymous Walk Embeddings（并没有深入研究）

五.怎么用这些Embedding？

六.知识表示

对于知识图谱中的一条边，可以用(h,r,t)来表示。其中，h和t表示实体，r表示关系。知识表示的目标是给定(h,r,t)，(h,r)的embedding和t的embedding是close的。这里的两个问题是：

（1）如何实现embedding？

（2）如何定义close？

这里的难点是关系模式的学习，典型的包括：对称关系，组合关系，1对N，N对1关系

这里的大框架定义的工作是从TransE开始的，后续各种TransX的工作，基本都没有脱离这种框架，同时Focus在各种复杂关系模式的学习上。

对于该方向上的工作，个人比较推荐MILA的Tang Jian的相关工作。