LeetCode终结:题解
为什么要有这份题解列表?
(1)由于博主尚没有养成时常做题的习惯,但是估计之后应该就能养成了。导致每次准备换工作的时候,都要重新梳理一遍题目,这样的效率比较低,因此这里想形成一个列表,之后如果有换工作的需求,就以此为纲。
(2)大厂的面试,尤其以字节和快手为例,特别强调代码题。比如快手的视频面试,直接是基于牛客网完成的,上来至少两道代码题,由面试官直接出题,编码之后要求通过测试例子。如果代码题不通过,之后的面试就不会进行了。另外,阿里的某些BU似乎都需要一轮代码题。
(3)自己作为面试官的题目准备。之前面过大概20+的候选人,一般代码题要求是口述(电面)或者现场白纸写代码,代码题也没有特别的准备,一般是临时找一些题,自己梳理完之后再去用到面试中去。(但是,个人感觉经常作为面试官的人,都会有一些自己的题库)
(4)代码题真的很能考验思维能力,有些题目也的确是非常的有意思,值得好好思考。
相关博客
3.重说:递归
4.重说:动态规划
7.再聊动态规划
8.两个Tricks
10.从最优装载看贪心
11.有趣的数据结构
12.系统设计题
13.字符串
14.Hash,值得拥有
####1.LRU(系统设计题)
class LRUCache(collections.OrderedDict):
def __init__(self, capacity: int):
super().__init__()
self.capacity = capacity
def get(self, key: int)->int:
if key not in self:
return -1#一般对于查找算法,找不到就返回-1
#访问过的元素向双向链表的头部移动
self.move_to_end(key)
return self[key]
def put(self, key: int, value: int)->None:
if key in self:
#访问过的元素向双向链表的头部移动
self.move_to_end(key)
self[key] = value
if len(self) > self.capacity:
self.popitem(last=False)#先进先出
####2.数据流中的中位数(系统设计题)
from heapq import *
class MedianFinder:
def __init__(self):
self.A = [] #小顶堆,保存较大的一半
self.B = [] #大顶堆,保存较小的一半
def addNum(self, num: int):
if len(self.A) != len(self.B):
heappush(self.A, num)
heappush(self.B, -heappop(self.A))
else:
heappush(self.B, -num)
heappush(self.A, -heappop(self.B))
def findMedian(self)->float:
return self.A[0] if len(self.A) != len(self.B) else (self.A[0] - self.B[0]) / 2.0
####3.二叉搜索树的增删查改
class TreeNode:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
class BinaryTree:
def insert(self, root, val):
if not root:
root = TreeNode(val)
elif val < root.val:
root.left = self.insert(root.left, val)
elif val > root.val:
root.right = self.insert(root.right, val)
return root
def search(self, root, val):
if not root:
return False
elif root.val > val:
return self.search(root.left, val)
elif root.val < val:
return self.search(root.left, val)
elif root.val == val:
return True
def modify(self, root, val, new_val):
if not root:
return False
elif root.val > val:
return self.modify(root.left, val, new_val)
elif root.val < val:
return self.modify(root.left, val, new_val)
elif root.val == val:
root.val = new_val
return True
#二叉搜索树的删除操作比之其他,相对复杂
def delete(self, root, key):
if not root:
return False
if root.val == key:
if not root.left and not root.right:return None
elif root.left == None:
root = root.left
elif root.right == None:
root = root.left
elif root.left and root.right:
#TODO
elif root.val > key:
root.left = self.delete(root.left, key)
elif root.val < key:
root.right = self.delete(root.right, key)
return root
3.1删除二叉搜索树中的节点
class Solution:
def successor(self, root):
root = root.right
while root.left:
root = root.left
return root
def predecessor(self, root):
root = root.left
while root.right:
root = root.right
return root
def deleteNode(self, root, key):
if not root: return None
if key > root.val:
root.right = self.deleteNode(root.right, key)
elif key < root.val:
root.left = self.deleteNode(root.left, key)
else:
if not root.left and not root.right:
root = None
elif root.right:#后继节点的值替代当前节点,删除后继节点
root.val = self.successor(root)
root.right = self.deleteNode(root.right, root.val)
else:
root.val = self.predecessor(root)#前继节点的值替代当前节点,删除前继节点
root.left = self.deleteNode(root.left, root.val)
return root
4.二叉树的遍历
#DFS(搜索): 前序,中序和后序
#BFS(搜索):层次
def pre_order(root):
if root:
print(root.val)
pre_order(root.left)
pre_order(root.right)
def in_order(root):
if root:
in_order(root.left)
print(root.val)
in_order(root.right)
#另外的写法
def in_order(root):
return in_order(root.left) + [root.val] + in_order(root.right) if root else []
def post_order(root):
if root:
post_order(root.left)
post_order(root.right)
print(root.val)
def layer_order(root):
queue = []
queue.append(root)
while len(queue) > 0:
node = queue.pop(0)
print(node.val)
if node.left:queue.append(node.left)
if node.right:queue.append(node.right)
TIPS:实现层次遍历二叉树,奇数层从左向右遍历,偶数层从右向左遍历
4.1N叉树的前序遍历
#前序遍历
def pre_order(root):
ans = []
if not root:
return ans
ans.append(root.val)
for child in root.children:#N叉树的构建需要children值
pre_order(child)
return ans
#对于后序遍历,直接对最后的结果取反即可
4.2N叉树的最大深度
def maxDepth(root):
if not root: return 0
elif len(root.children) == 0:
return 1
else:
height = [maxDepth(c) for c in root.children]#对于每个children求深度
return max(height) + 1
4.3二叉树的直径
def maxDepth(root):
#二叉树的最大深度
if not root: return 0
return 1 + max(maxDepth(root.left), maxDepth(root.right))
def getDiameter(root):
if not root: return 0
res = maxDepth(root.left) + maxDepth(root.right) + 1#穿过root节点
return max(res, getDiameter(root.left), getDiameter(root.right))#不穿过root节点,分别在左右子树中
4.4二叉树交换左右子树
def exchange_tree(root):
if not root:
return False
else:
if root.left and root.right:
root.left, root.right = root.right, root.left
exchange_tree(root.left)
exchange_tree(root.right)
5.单链表反转
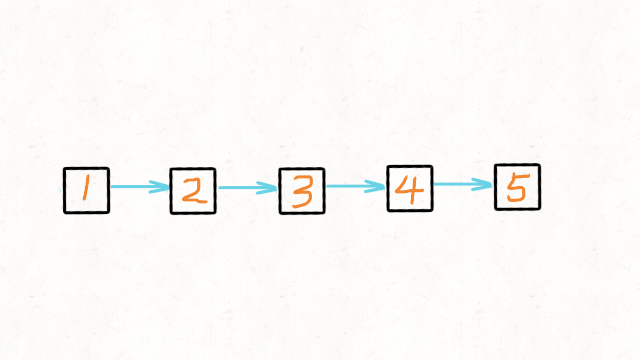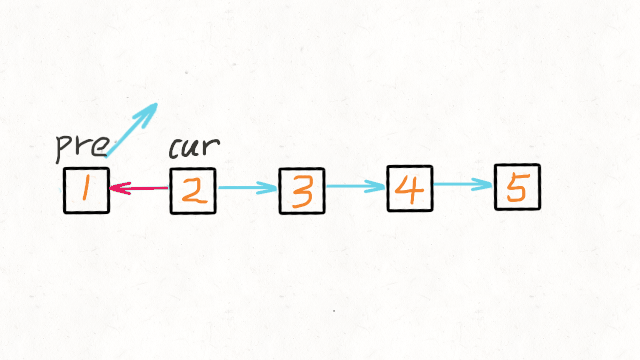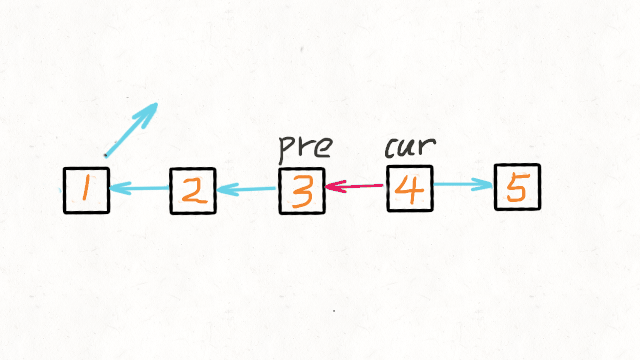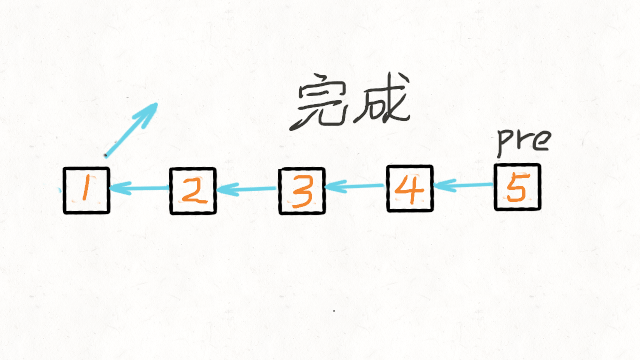
def reverseList(head):
pre = None
cur = head
while cur:
tmp = cur.next
cur.next = pre
pre = cur
cur = tmp
return pre
6.合并两个有序链表
def mergeTwoLists(l1, l2):
if not l1: return l2
if not l2: return l1
if l1.val <= l2.val:
l1.next = mergeTwoLists(l1.next, l2)
return l1
else:
l2.next = mergeTwoLists(l1, l2.next)
return l2
7.判断链表中是否有环
def hasCycle(head):
if not head or not head.next: return False
slow = head
fast = head.next
while slow != fast:
if not fast or not fast.next:#单链表,没有环
return False
slow = slow.next#慢指针每次走一步
fast = fast.next.next#快指针每次走两步
return True
7.1链表倒数第K个节点
7.2删除排序链表中的重复元素
7.3链表公共节点
8.二分查找
def search(nums, target):
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
elif nums[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1#查找算法,找不到,返回-1
9.快速排序
def quick_sorted(nums, left, right):
if left >= right: return nums
#以数组的第一个节点作为pivot
pivot = nums[left]
#记录数组的左右两边
low = left
high = right
while left < right:
while left < right and nums[right] >= pivot:
right -= 1
nums[left] = nums[right]
while left < right and nums[left] < pivot:
left += 1
nums[right] = nums[left]
#right和left指向相同位置
nums[right] = pivot
quick_sort(nums, low, left - 1)
quick_sort(nums, left + 1, high)
10.连续子数组的最大和

def maxSubArray(nums):
for i in range(1, len(nums)):
nums[i] += max(nums[i-1], 0)
return max(nums)
11.全排列
def permutations(nums, start, end):
if start == end:
return nums
else:
for i in range(start, end):
nums[i], nums[start] = nums[start], nums[i]
permutations(nums, start + 1, end)
nums[i], nums[start] = nums[start], nums[i]
TIPS:组合问题呢?
12.斐波那契数列和爬楼梯
#递归式的解法
def fibonacci(n):
if n <= 0:
return 0
if n == 1:
return 1
return fibonacci(n-1) + finonacci(n-2)
#迭代式的解法
#用两个变量存储
def finonacci(n):
first, second = 0,1
for _ in range(2,n):
first, second = second, first + second
return first
#用一个数组存储
def finonacci(n):
ans = []
ans[0] = 0
ans[1] = 1
for i in range(2, n):
ans[i] = ans[i-1] + ans[i-2]
return ans[n-1]
13.两个栈实现队列
基础语法:
a = [1,2,3]
a.pop()#3
a#[1,2]
a.pop(0)#1
a#[2]
class CQueue:
def __init__(self):
self.A = []
self.B = []
def appendTail(self, value: int)->None:
self.A.append(value)
def deleteHead(self)-> int:
if self.B: return self.B.pop()
if not self.A: return -1
while self.A:
self.B.append(self.A.pop())
return self.B.pop()
14.两个队列实现栈
基础语法:
import collections
data = collections.deque()#双端队列
data.append(1)
data.append(2)
data.append(3)
data.popleft()#1,原地操作
data.popright()#3,原地操作
class CStack:
def __init__(self):
self.A = []
self.B = []
def push(self, value:int)->None:
self.B.append(value)
while self.A:
self.B.append(self.A.pop(0))
#交换操作
self.A, self.B = self.B, self.A
def pop(self)->int:
return self.A.pop(0)
def top(self)->int:
retrun self.A[0]
def empty(self)->bool:
return not self.A
15.N数之和
#两数之和
def twoSum(nums, target):
hashtable = {}
for i, num in enumerate(nums):
if target - num in hashtable:#判断是否在hashtable中
return [hashtable[target-num],i]
hashtable[nums[i]] = i
return []#找不到的时候,返回空
16.第K大元素
import heapq
def findKthLargest(nums, k)->int:
#python中默认的是小顶堆,入堆和出堆取负
nums = [-1 * num for num in nums]
#将一个数组堆化
heapq.heapify(nums)
for _ in range(k-1):
heapq.heappop(nums)#操作对象是数组
return -1 * heapq.heappop(nums)
16.1.数组中前K个高频元素
def topKFrequent(nums, k):
return [e[0] for e in collections.Counter(nums).most_common(k)]
def topKFrequent(nums, k):
dic = collections.Counter(nums)
heap, ans = [], []
for i in dic:
heapq.heappush(heap, (-dic[i],i))
for _ in range(k):
ans.append(heapq.heappop(heap)[1])
return ans
17.最长公共子串
def longestCommonSubstr(str1, str2)->int:
def dp(i,j):
if i == -1 or j == -1:
return 0
if str1[i] == str2[j]:
return dp(i-1, j-1) + 1
else:
return 0#子串和子序列的区别
return dp(len(str1)-1, len(str2)-1)
18.最长公共子序列
def longestCommonSubsequence(str1, str2)->int:
def dp(i,j):
if i == -1 or j == -1:
return 0
if str1[i] == str2[j]:
return dp(i-1, j-1) + 1
else:
return max(dp(i-1,j), dp(i,j-1))#子串和子序列的区别
return dp(len(str1)-1, len(str2)-1)
TIPS:如果要返回找到的子串和子序列呢?
19.最长回文串
题目描述:给定一个包含大写字母和小写字母的字符串,找到通过这些字母构造成的最长的回文串。
输入:"abccccdd"
输出:7
解释:我们可以构造的最长的回文串是"dccaccd", 它的长度是7
#频数统计:count
def longestPalindrome(s)->int:
ans = 0
for c in set(s):
count = s.count(c)
if count % 2 == 0:
ans += count
elif count % 2 != 0 and count > 2:
ans += count-1
#回文串中间的一个字符
if len(s) > res:
res += 1
return ans
20.编辑距离
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
#初始化dp数组
m, n = len(word1)+1, len(word2)+1
dp = [[0 for _ in range(n)] for _ in range(m)]
#dp数组的边界
for i in range(m):
dp[i][0] = i
for j in range(n):
dp[0][j] = j
#计算dp数组的值
for i in range(1, m):
for j in range(1, n):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = 1 + min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j])#修改,增加和删除
return dp[m-1][n-1]
21.最长不含重复字符的子字符串
#滑动窗口
def lengthOfLongestSubstring(s: str)->int:
head=tail=0
ans = 1
if len(s) < 2: return len(s)
while tail < len(s) - 1:
tail += 1
if s[tail] not in s[head:tail]:
ans = max(tail-head+1, ans)
else:
while s[tail] in s[head:tail]:
head += 1
return ans
22.最长上升子序列
#状态转移方程:dp[i] = max(dp[j]) + 1,其中0 <= j < i 且nums[j] < nums[i]
#结果:max(dp[i]),其中0 <= i < n
def lengthOfLIS(nums)->int:
if not nums: return 0
dp = [1 for _ in len(nums)]
for i in range(len(nums)):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[j]+1, dp[i])
return max(dp)
23.验证是否是二叉搜索树
def isValidBST(root):
def dfs(node, min_val, max_val):
if not node: return True
if not min_val < node.val < max_val:
return False
return dfs(node.left, min_val, node.val) and dfs(node.right, node.val, max_val)
return dfs(root, float("-inf"), float("inf"))
24.两数相加(链表)
class Solution:
def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
# 创建一个结点值为 None 的头结点, dummy 和 p 指向头结点, dummy 用来最后返回, p 用来遍历
dummy = p = ListNode(None)
s = 0 # 初始化进位 s 为 0
while l1 or l2 or s:
# 如果 l1 或 l2 存在, 则取l1的值 + l2的值 + s(s初始为0, 如果下面有进位1, 下次加上)
s += (l1.val if l1 else 0) + (l2.val if l2 else 0)
p.next = ListNode(s % 10) # p.next 指向新链表, 用来创建一个新的链表
p = p.next # p 向后遍历
s //= 10 # 有进位情况则取模, eg. s = 18, 18 // 10 = 1
l1 = l1.next if l1 else None # 如果l1存在, 则向后遍历, 否则为 None
l2 = l2.next if l2 else None # 如果l2存在, 则向后遍历, 否则为 None
return dummy.next # 返回 dummy 的下一个节点, 因为 dummy 指向的是空的头结点, 下一个节点才是新建链表的后序节点
25.对称二叉树
def isSymmetric(root):
if not root: return True
def isSym(root1, root2):
#和判断两棵树是否相同的逻辑类似,区别在于递归部分代码
if not root1 and not root2:
return True
if root1 and root2 and root1.val == root2.val:
return isSym(root1.left, root2.right) and isSym(root1.right, root2.left)
return False
return isSym(root.left, root.right)
25.翻转二叉树
def invertTree(root):
if not root: return root
left = invertTree(root.left)
right = invertTree(root.right)
root.left, root.right = right, left
return root
TIPS:分析树递归的好题目
26.搜索旋转排序数组
def search(nums, target):
if not nums: return -1
l, r = 0, len(nums)-1
while l <= r:
mid = (l+r)//2
if nums[mid] == target:
return mid
if nums[0] <= nums[mid]:
if nums[0] <= target < nums[mid]:
r = mid - 1
else:
l = mid + 1
else:
if nums[mid] < target <= nums[len(nums)-1]:
l = mid + 1
else:
r = mid -1
return -1
27.最长公共前缀
def longestCommonPrefix(strs):
res = ""
for tmp in zip(*strs):
tmp_set = set(tmp)
if len(tmp_set) == 1:
res += tmp[0]
else:
break
return res
28.一棵树是否是另一棵树的子树
def isSubtree(s, t):
if not s and not t: return True
if not s or not t: return False
retrun self.isSameTree(s,t) or isSubtree(s.left, t) or isSubtree(s.right, t)
def isSameTree(s,t):
#判断两棵树是否相同
if not s and not t: return True
if not s or not t: return False
return s.val == t.val and isSameTree(s.left, t.left) and isSameTree(s.right, t.right)
29.单调栈相关
#下一个更大的元素
def nextGreaterElement(nums):
stack = []
res = [-1] * len(nums)
for i, n in enumerate(nums):
while stack and nums[stack[-1]] < n:
res[stack.pop()] = n
stack.append(i)
return res
#前一个更大的元素
def preGreaterElement(nums):
stack = []
res = [-1] * len(nums)
for i, n in enumerate(nums):
while stack and nums[stack[-1]] < n:
stack.pop()
if stack:
res[i] = nums[stack[-1]]
stack.append(i)
return res
#下一个更小的元素
def nextSmallerElement(nums):
stack = []
res = [-1] * len(nums)
for i, n in enumerate(nums):
while stack and nums[stack[-1]] > n:
res[stack.pop()] = n
stack.append(i)
return res
#前一个更小的元素
def preSmallerElement(nums):
stack = []
res = [-1] * len(nums)
for i, n in enumerate(nums):
while stack and nums[stack[-1]] > n:
stack.pop()
if stack:
res[i] = nums[stack[-1]]
stack.append(i)
return res
30.大数加法/相乘
#大数相加
def addStrings(num1: str, num2: str)->str:
s1 = list(num1)[::-1]
s2 = list(num2)[::-1]
carry = 0
res = []
i = 0
while i < len(s1) or i < len(s2) or carry:
n1 = int(s1[i]) if i < len(s1) else 0
n2 = int(s2[i]) if i < len(s2) else 0
#返回商和余数
carry,n = divmod(n1+n2+carry,10)
res.append(str(n))
i += 1
return "".join(res[::-1])
#大数相乘
def multiply(num1: str, num2: str)->str:
if num1 == "0" or num2 == "0":
return "0"
result = 0
num1 = num1[::-1]
num2 = num2[::-1]
for i, x in enumerate(num1):
tmp = 0
for j, y in enumerate(num2):
tmp += int(x) * int(y) * 10 ** j
result += tmp * 10 ** i
return str(result)
31.驼峰命名法转下划线
def get_trans_name(text):
length=len(text)
lst=[]
for i in range(length):
# 前一个字母大写,后一个字母小写,将该字母从大写转换成小写
if i+1<length and text[i].isupper() and not text[i+1].isupper():
lst.append(text[i].lower())
else:
lst.append(text[i])
# 前一个字母是小写,后一个字母是大写的情景
if not text[i].isupper() and i+1<length and text[i+1].isupper():
lst.append("_")
# 前两个字母是大写,后一个字母是小写的情景
if text[i].isupper() and i+2<length and text[i+1].isupper() and not text[i+2].isupper():
lst.append("_")
return "".join(lst)
32.移除K位数字
def removeKdigits(num, k):
stack = []
remain = len(num)-k
for digit in num:
while k and stack and stack[-1] > digit:
stack.pop()
k -= 1
stack.append(digit)
return "".join(stack[:remain]).lstrip("0")#合法的数字要去掉之前的“0”
TIPS:单调栈问题
33.双指针的基础经典题
TIPS: 以单链表为主的快慢指针问题+以二分查找为主的左右指针