图划分
在基于图的目标函数分解策略中,已经相对详细的说了目标函数分解的方法,本文则谈计算的问题。
0. 同步,异步,阻塞,非阻塞
同步是指调用者没有从被调用者那里得到结果前,调用者不返回。
异步是指调用者发出调用后就返回(没有结果),当有结果时,被调用者告诉调用者。
阻塞是在没有获得结果前,调用者一直等待,啥也不干。
非阻塞是在没有获得结果前,调用者去干别的事情,时不时查询一下被调用者是否返回结果。
[一个字一个字儿读]
从上述关系上来看,同步和异步反映调用者和被调用者之间的关系,或者说反映了二者之间的消息通信机制,阻塞和非阻塞描述的是调用者的状态,异步一定是非阻塞,但是调用者获取结果的方式不同,对异步来说,是调用者被动接受(由被调用者发出”有结果啦”的消息),而非阻塞是调用者主动获取(时不时问被调用者,”有结果没呢?”)。但是同步是可以分为阻塞和非阻塞的,注意同步和非阻塞的关系,调用者不返回和调用者去干别的事情不冲突的。
关于上述概念更丰富的理解,可以见这里。
1. MPI通信
1.0 MPI_Barrier
这里有一个Demo,我尝试说形象地表达一下。A,B,C三个同学跑5000米,有个教练D,为了保证最终A,B,C的成绩差距不太大,他在1000米处等着,三个同学没有全到达该处时,其他任意一个到的同学要等待其他同学,然后开跑。”在1000米处等”就意味着设置了一个Barrier,不管Barrier前各个任务的执行速度,先来的都要等待后到的,在后续的RDPSO的分布式计算中可以使用Barrier实现(粗粒度)同步计算。
1.1 MPI_Send和MPI_Recv,MPI_ISend和MPI_IRecv
Send和Recv是用于阻塞通信,而ISend和IRecv用于非阻塞通信,通过设置消息缓冲区实现计算和通信的重叠。这里很显然,消息缓冲区的大小会成为一个bottleneck。代码先占坑:
#include<mpi.h>
#include<stdio.h>
int main(int argc ,char * argv[]){
int s1=5 ,r1=4;
MPI_Status status;
MPI_Request req;
int nprocs,rank;
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
if(rank==0){
//MPI_Send(&s1,1,MPI_INT,1,1,MPI_COMM_WORLD);
MPI_Isend(&s1, 1, MPI_INT, 1, 1, MPI_COMM_WORLD, &req);
MPI_Wait(&req, &status);
printf("rank 0 send!\n");
}
if(rank==1){
//MPI_Recv(&r1,1,MPI_INT,0,1,MPI_COMM_WORLD,&status);
MPI_Irecv(&r1, 1, MPI_INT, 0, 1, MPI_COMM_WORLD, &req);
MPI_Wait(&req, &status);
printf("rank 1 recv!\n");
printf("recv data: %d\n",r1);
}
MPI_Finalize();
return 0;
}
使用非阻塞通信时,需要显式调用MPI_Wait,为了测试非阻塞效果,可以通过传输大量的数据,来看是否影响程序下一行代码地执行,在测试中开辟了稍微大的空间就会挂掉,难道技能点还没Get到(需要明确应用场景)?
1.2 集合通信
集合操作的三种类型包括:同步,数据传递(广播,分散,收集等),规约。具体可以参照这篇文章,想来与神威太湖之光也就一墙之隔。
1.3 Allreduce
在之前的文章中多次提到工业界对于SGD的分布式优化通常的思路是MPI+AllReduce+SGD,所以这里着重提一下MPI_Reduce和MPI_Allreduce,下述内容参照该tutorial,良心文档,安利一发。
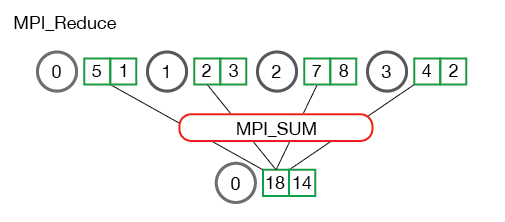
关键代码:
// Reduce all of the local sums into the global sum
float global_sum;
MPI_Reduce(&local_sum, &global_sum, 1, MPI_FLOAT, MPI_SUM, 0,
MPI_COMM_WORLD);
// Print the result
if (world_rank == 0) {
printf("Total sum = %f, avg = %f\n", global_sum,
global_sum / (world_size * num_elements_per_proc));
}
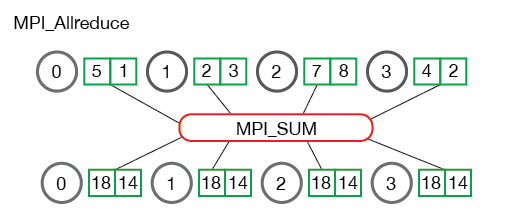
关键代码:
// Reduce all of the local sums into the global sum in order to
// calculate the mean
float global_sum;
MPI_Allreduce(&local_sum, &global_sum, 1, MPI_FLOAT, MPI_SUM,
MPI_COMM_WORLD);
float mean = global_sum / (num_elements_per_proc * world_size);
对比二者的区别:MPI_Allreduce=MPI_Reduce+MPI_Bcast.从代码中可以看到MPI_Reduce之后,global_sum在root process(根节点,主节点,管理节点)被访问,其他(计算)节点不可访问,而MPI_Allreduce则可以在计算节点上访问global_sum。类似的还有MPI_Allgather和MPI_Gather两个操作,MPI_Allgather=MPI_Gather+MPI_Bcast,从操作上来看,Reduce和Gather有什么区别呢?
Gather重在数据的收集,对于收发两端的数据起始地址,数据个数和数据类型敏感,Reduce重在数据的处理,故在MPI_Reduce的API中有MPI_Op这个关键的操作参数(MPI_MAX,MPI_SUM,MPI_MAXLOC,MPI_MINLOC等)。
2. 计算实现
下图是目标函数分解后的通信拓扑:

Rosenbrock’s function如下:
\[F=\sum_{i=1}^{D-1}(100(x_{i}^2-x_{i+1})^2+(x_{i}-1)^2)+bias\]令D=6(变量维度),K=3(子目标个数),由于是按照SUM方式分解,每个子目标的和就是原目标。如上图,红色圆圈表示子目标f1,绿色表示子目标f2,紫色表示子目标f3,由分解结果知道,f1和f2的依赖变量是x1,f2和f3的依赖变量是x3。如何利用RDPSO算法寻找原函数的最小值?据老板说,他搞的这个算法在稳定性上比较好,具体没有研究过。
整体的思路是:给集群的每个计算节点上分配一个粒子群用来优化对应的子函数f,设置子种群迭代次数sub_iter,当子种群迭代次数到达该值时(目前假定f1,f2,f3同时到达),f1和f2交换x1的值,f2和f3交换x3的值,交换后的值作为下一次迭代的粒子初始值,相比于首次迭代开始,粒子初始值是随机值。设置种群迭代次数max_iter,也就是子种群互相交互的次数,当达到该值时,在管理节点上得到每个子种群的粒子位置gbestx和对应的最优值gbest,所有子种群的gbest求和作为全局gbest。
实际上在上述策略中,涉及的关键问题是冲突变量的解决。围绕着交换冲突(共享)变量的目标,要解决两个问题,第一是when?在假设子目标寻优同时结束的情况下,策略如上描述,这是一种同步方案。可是假设子目标函数的差别较大,子目标寻优不同时结束时情况怎样?其中一种情况是f2和f1以及f3都有x1的依赖,如何处理关于x1的更新呢?显然此时需要为x1加锁,但是会不会由于同步方案的选择造成计算效率的降低?第二是how?在上述策略描述中,简单的做exchange,如何评估方案的好坏?比如说更好的加权方案,满足某种映射关系?
代码还没有整理,雏形阶段,不是对这个问题感兴趣,一定不要点开。Github代码