[LeetCode]NP问题和近似算法

P，NP，NPC问题的关系：

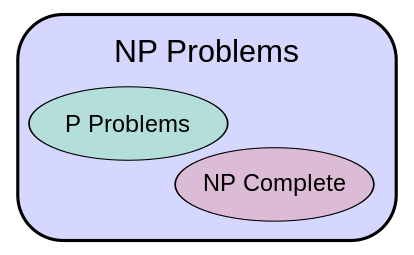
上图是假设P != NP的情形，如果P = NP，则P = NP = NPC

NPC问题没有多项式时间算法，常用解题策略：

1. 只计算特殊情况下的解

2. 动态规划或分支限界求解

3. 概率算法

4. 近似解

5. 启发式求解

四个NPC问题的近似算法的例子：

顶点覆盖问题

问题描述：给定一个N个点M条边的无向图G（点的编号从1至N），问是否存在一个不超过K个点的集合S，使得G中的每条边都至少有一个点在集合S中。

近似算法思想：从G中的所有边中任选一条边，删除与该边两端顶点连接的所有边。从剩余边中继续任意选择第二条边，删除与该边两端顶点连接的所有边。继续该过程，直到没有剩余边可以选择，这时被选择的边的所有两端顶点就是集合S中的元素。

算法执行过程如下图：

图(e)是近似算法得出的集合S，其中元素包括：

b，c，d，e，f，g

图(f)是含有最少点的集合S(通常意味着最优),元素包括：

b，e，d

旅行售货员问题

问题描述：给定一个完全无向图G=(V,E)，其每一边(u,v)∈E有一非负整数费用c(u,v)，要找出G的最小费用哈密顿回路。

一个性质（三角不等式）：费用函数c通常意义下具有三角不等式性质，即对任意的3个顶点u,v,w∈V，有：c(u,w)≤c(u,v)+c(v,w)。

近似算法思想：从G中任选一个点A，用Prim算法做以A为根的最小生成树T，前序遍历T得到顶点表L，将A加入L的末尾，最后按照L中顶点次序连接得到目标回路。

算法执行过程如下图：

—

图(d)是近似算法的结果，图(e)是最优结果。

集合覆盖问题

问题描述：给定一个集合U以及U内元素构成的若干各小类集合S，目标是找到S的一个子集，该子集满足所含元素包含了所有的元素且使小类集合个数最少。

例如，U={1,2,3,4,5}，S=[{1,2},{3,4},{2,4,5},{4,5}],找到集合能满足条件的可以有”[{1,2},{3,4}{4,5}]”或是”[{1,2},{3,4},{2,4,5}]。

近似算法(贪婪思想)，伪代码描述如下：

/**
* X: 全体元素的集合
* F: 由X中元素构成的小类集合的集合
*/
Set greedySetCover(X,F)
{
   U=X；
   C=NULL；
   while (U != NULL) {
     选择F中使|S∩U|最大的子集S；
     U=U-S；
     C=C∪{S}；
     }
   return C；
} 

近似算法采用贪心思路，每次选择与全体元素集合交集最大的子集合。这样的决策从当前看来，可以减少最终结果的子集合数目。因为可以简单地理解为，在最终得到的子集合中，元素（是一个集合）越大，元素个数越少，因为子集合中元素(集合)的并是全体元素(个体)。

子集和问题

问题描述：S={x1，x2，…，xn}是一个正整数的集合，t是一个正整数。子集和问题判定是否存在S的一个子集S1，使得S1中的元素和等于t。

指数时间算法伪代码如下：

int exactSubsetSum(S,t)
{
    int n=|S|；
    L[0]={0}；
    for(int i=1；i<=n；i++) {
        L[i]=mergeLists(L[i-1],L[i-1]+S[i])；
        删去L[i]中超过t的元素；
    }
    return max(L[n])；
}

完全多项式时间近似格式

基于算法exactSubsetSum，通过对表L[i]作适当的修整建立一个子集和问题的完全多项式时间近似格式 在对表L[i]进行修整时，用到一个修整参数δ，0＜δ＜1。用参数δ修整一个表L是指从L中删去尽可能多的元素，使得每一个从L中删去的元素y，都有一个修整后的表L1中的元素z满足(1-δ)y≤z≤y可以将z看作是被删去元素y在修整后的新表L1中的代表。

修正算法伪代码：

List trim(L,δ)
{  
    int m=|L|；
    L1=〈L[1]〉；
    int last=L[1]；
    for(int i=2；i<=m；i++) {
        if(last<(1-δ)*L[i]) {//另一种表达：last*(1+δ)<L[i]
            将L[i]加入表L1的尾部；
            last=L[i]；
        }
    return L1；    } 

改正后子集合问题的完全多项式时间格式伪代码：

int approxSubsetSum(S,t,ε)
{
    n=|S|；
    L[0]=〈0〉；
    for(int i=1；i<=n；i++) {
        L[i]=Merge-Lists(L[i-1],
        L[i-1]+S[i])； 
        L[i]=trim(L[i],ε/n)；//此处添加trim操作
        删去L[i]中超过t的元素；
    }
    return max(L[n])；
} 

衡量NPC问题的近似解法的最重要的两个性能指标：时间复杂度和近似比(当然并不是意味着空间复杂度不重要)。关于上述四个问题的性能评估，并不是本文的目标。数学色彩更加浓厚的文章可能对于时间复杂度和近似比这两件事儿说的相对清晰一些。